【考研自控】题型解法一:Nyquist曲线图与判据
【考研自控】题型解法一:Nyquist曲线图与判据
本题一般会给一个开环传递函数G(s),根据开环传递函数画Nyquist曲线。
步骤一:分析开环传递函数
得到的开环传递函数一般如下所示:
$$G(s) = {{K\mathop \prod \limits_{i = 1}^m ({\tau _i}s + 1)} \over {{s^v}\mathop \prod \limits_{i = 1}^n ({T_i}s + 1)}} = {{K({\tau _1}s + 1)({\tau _2}s + 1) \cdots } \over {{s^v}({T_1}s + 1)({T_2}s + 1) \cdots }}$$当你看到传递函数需要画奈氏图的时候,你需要一眼分析出以下信息:
- 此传递函数为几型系统:由开环传递函数中的确定;
- 开环传递函数的零极点与个数:
- 零点:令;
- 极点:令;
- 零点个数为,极点个数为。
- 判断该传递函数的环节(如积分环节、微分环节等)。
步骤二:求幅相率特性函数G(jω)
令,并带入开环传递函数,并经过整理可以得到复数函数,分别令实部为,虚部为形如:
$$G(j\omega ) = U(\omega ) + jV(\omega )$$若开环传递函数由若干典型环节相串联:,还可化为以下形式,
$$G(j\omega ) = |{G_1}(j\omega )||{G_2}(j\omega )| \cdots |{G_n}(j\omega )|{e^{j[\angle {G_1}(j\omega ) + \angle {G_2}(j\omega ) + \cdots + \angle {G_n}(j\omega )]}}$$其中可以得到幅频和相频分别为:
$$\eqalign{ & A(\omega ) = |{G_1}(j\omega )||{G_2}(j\omega )| \cdots |{G_n}(j\omega )| \cr & \varphi (\omega ) = \angle {G_1}(j\omega ) + \angle {G_2}(j\omega ) + \cdots + \angle {G_n}(j\omega ) \cr} $$例如传递函数,可求得:
$$A(\omega ) = {{K\sqrt {({\omega ^2} + 1)} } \over {\omega \sqrt {(4{\omega ^2} + 1)} \sqrt {({\omega ^2} + 4)} }}$$ $$\varphi (\omega ) = - \arctan ({\omega \over 0}) - arctan({{2\omega } \over 1}) - arctan({\omega \over { - 2}}) + arctan({\omega \over 1})$$注:若已确定为型系统,可直接将替换为。最终整理为以下的公式:
$$\varphi (\omega ) = - {90^ \circ } - arctan(2\omega ) - arctan({\omega \over { - 2}}) + arctan(\omega )$$步骤三:绘制Nyquist曲线
首先确定增补线,若开环传递函数包含积分环节,应从对应的点开始,补做一个半径为无穷,逆时针方向旋转的大圆弧增补线,把它视为Nyquist曲线的一部分。再确定奈氏图的起点,令,求奈氏图起点角度与距离:
$${A_1} = \mathop {\lim }\limits_{\omega \to 0} A(\omega ),{\theta _1}{\rm{ = }}\mathop {\lim }\limits_{\omega \to {0^ + }} \varphi (\omega )$$确定奈氏图终点,令,求奈氏图终点角度与距离:
$${A_2} = \mathop {\lim }\limits_{\omega \to + \infty } A(\omega ),{\theta _2}{\rm{ = }}\mathop {\lim }\limits_{\omega \to + \infty } \varphi (\omega )$$确定奈氏图与实轴的交点,方便以后的Nyquist判据,令,求出,再带入,即可得与实轴的交点。并根据以上信息可以画出奈氏图的大致曲线。
步骤四:利用Nyquist判定系统的稳定性(若题目要求)
首先列出稳定性判据:通过绘制的从时的开环幅相特性曲线(奈氏图),按其包围的圈数(逆时针为正,顺时针为负)和开环传递函数在右半平面根的个数,根据公式:
$$Z = P - 2N$$来确定闭环特征方程正实部根的个数。若,闭环系统是稳定的,否则闭环系统不稳定。
将增补线作为奈氏图的一部分,分别利用以下穿越类型来确定圈数:
- 正穿越:随着的增大,开环幅相曲线逆时针(由上到下)穿越点左侧的负实轴,记为一次正穿越,计数为正,记为。
- 负穿越:随着的增大,开环幅相曲线顺时针(由下到上)穿越点左侧的负实轴,记为一次负穿越,计数为负,记为。
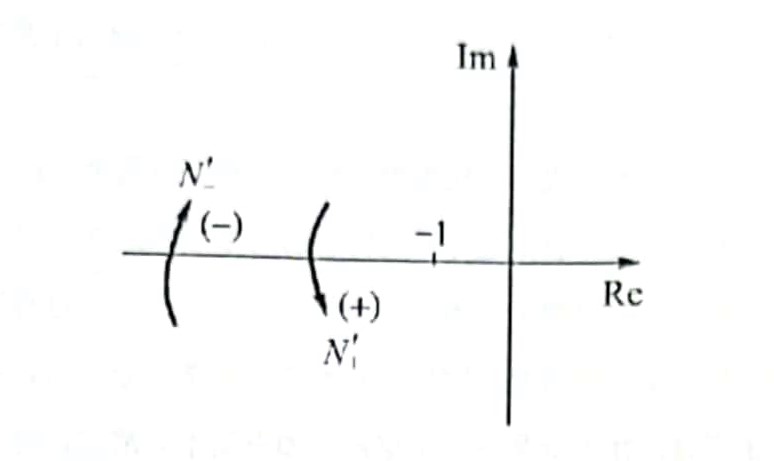
- 半次穿越:开环幅相曲线起始于(或终止于)点左侧的负实轴,若沿逆时针方向离开(或终止于)负实轴,记为半次正穿越,用表示;若沿顺时针方向离开(或终止于)负实轴,记为半次负穿越,用表示;
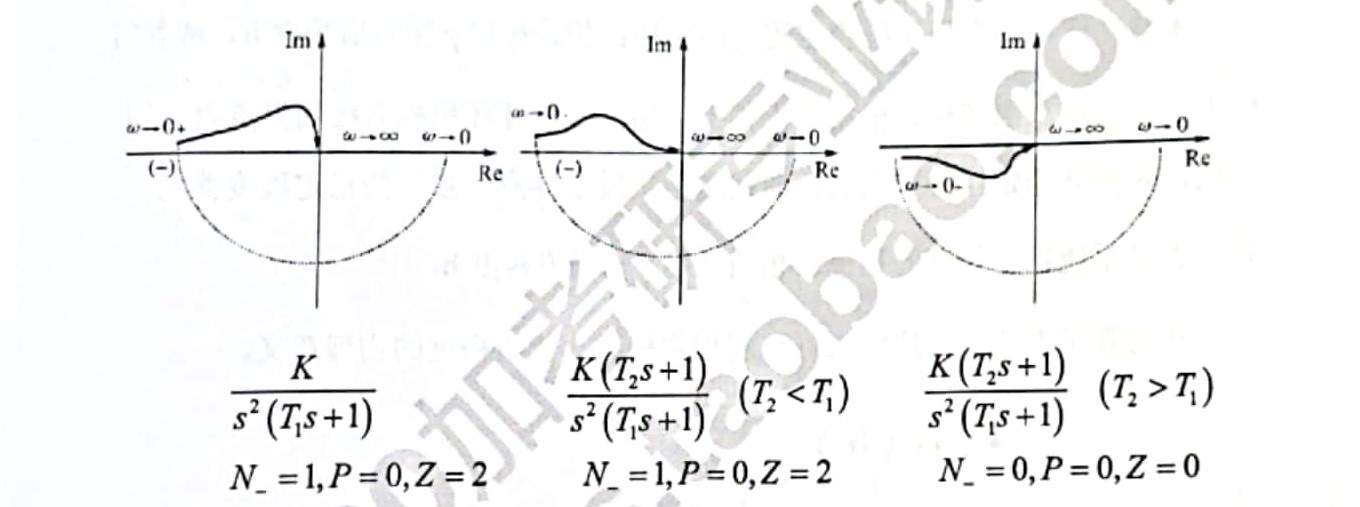
可参考以下示例进行判断:
经典真题
题目:(北航933,2010,三)已知某单位负反馈系统开环传递函数为:
$$G(s) = {{2(s + 1)} \over {s(s - 1)}}$$- 画开环Nyquist曲线;
- 利用Nyquist判据判断系统闭环稳定性。
解答:(1)令,得到:
$$\eqalign{ & G(j\omega ) = {{ - 2 - 2\omega } \over {{\omega ^2} + 1}} + j{{2 - 2{\omega ^2}} \over {{\omega ^3} + \omega }} \cr & A(\omega ) = {{2\sqrt {({\omega ^2} + 1)} } \over {\omega \sqrt {{\omega ^2} + 1} }} \cr & \varphi (\omega ) = - {90^ \circ } - \arctan ( - \omega ) + \arctan (\omega ) \cr} $$其中,当时:
$$\mathop {\lim }\limits_{\omega \to {0^ + }} A(\omega ) = \infty ,\mathop {\lim }\limits_{\omega \to {0^ + }} \varphi (\omega ) = - {270^ \circ }$$当是,有:
$$\mathop {\lim }\limits_{\omega \to \infty } A(\omega ) = 0,\mathop {\lim }\limits_{\omega \to \infty } \varphi (\omega ) = - {90^ \circ }$$求曲线与实轴的交点,令
$$V(\omega ) = {{2 - 2{\omega ^2}} \over {{\omega ^3} + \omega }} = 0 \Rightarrow \omega = 1$$将求出的带入实部得到交点:
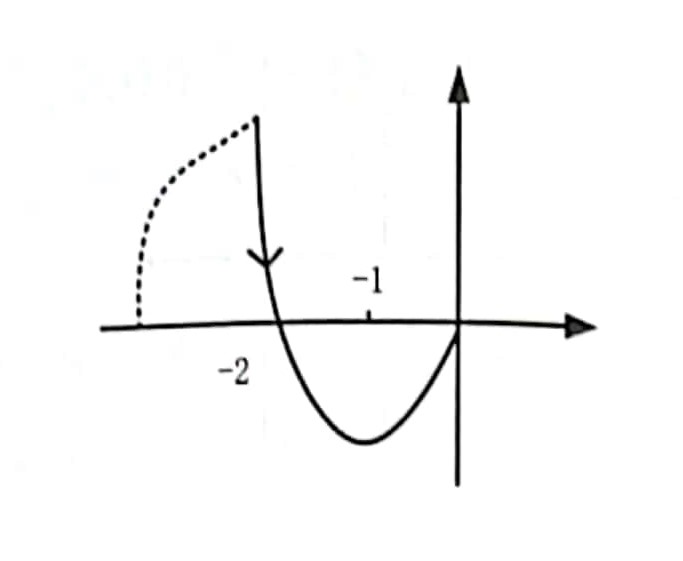
$$U(1) = {{ - 2 - 2} \over {1 + 1}} = - 2$$因为存在积分环节且,则增补线起始点应该在实轴的负半轴上,则Nyquist曲线图如下所示:
(2)由Nyquist曲线图进行分析,曲线与实轴交点为,包含点,曲线起始于点左侧的负实轴,并逆时针穿越负实轴,因为记为半次穿越,则;开环传递函数右半平面根的个数,根据公式,,因此闭环系统稳定。