【学术】4-麦克纳姆轮平台运动学建模
1. 单个麦克纳姆轮运动模型
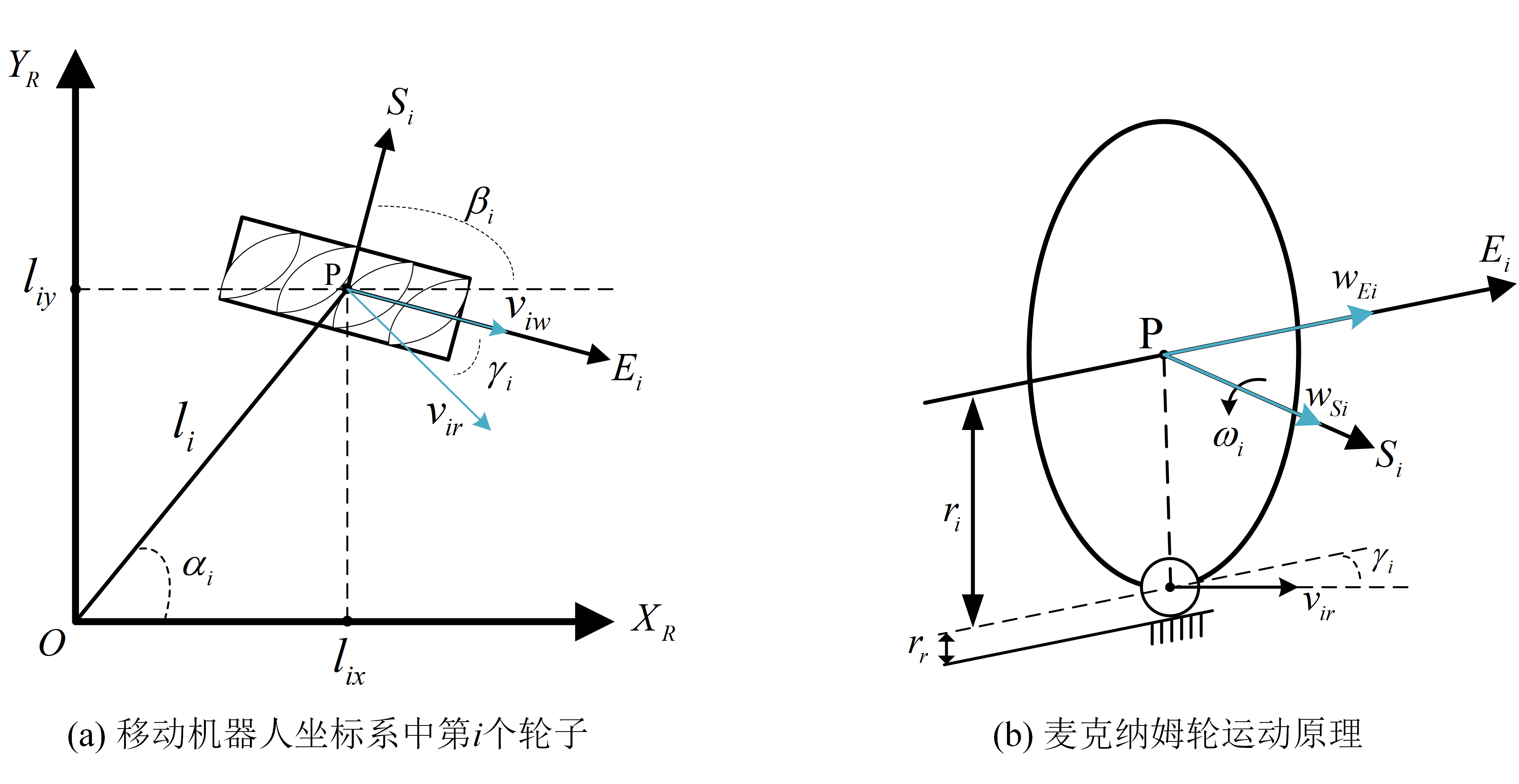
麦克纳姆轮由一个轮毂与多个辊子构成的异形轮,其中麦克纳姆轮轮轴与辊子滚轴夹角为45°。如图1.1(a)所示,在麦克纳姆轮转动时,辊子将与地面进行摩擦并产生特殊的速度分量,为垂直于辊子的速度[1]。
可以根据图1.1(b)可以计算出车轮产生的前向速度分量与自由辊子与地面所接触的切向速度,并满足公式(4-1)。
$$
{v_{ir}} = \frac{1}{{\cos {{45}^ \circ }}}{r_r}{\omega _i},\:{w_{Ei}} = {r_i}{\omega _i},\:i = 1,2,3,4\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4-1)
$$
同时根据图1.1(b)可以求出单个轮子的平面坐标系上的速度分量,他们分别用与来表示,并整理出式(4-2)。
$$
\left[ {\begin{array}{*{20}{c}}
{{v_{Si}}}\\
{{v_{Ei}}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
0&{\sin {\gamma _i}}\\
{{r_i}}&{\cos {\gamma _i}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{\omega _i}}\\
{{v_{ir}}}
\end{array}} \right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4-2)
$$
2. 单个麦轮运动模型转移
在上一节中我们得到了单个麦克纳姆轮的运动模型和速度分量,现在我们将它的速度分量转移到平台中心坐标系。根据图1.1(a)中可以将单个轮子的平面坐标系转变为移动机器人中心点的坐标系,并得到机器人平台速度分量与的关系式(4-3)。
$$
\left[ {\begin{array}{*{20}{c}}
{{v_{Xi}}}\\
{{v_{Yi}}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\cos {\beta _i}}&{ - \sin {\beta _i}}\\
{\sin {\beta _i}}&{\cos {\beta _i}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{v_{Si}}}\\
{{v_{Ei}}}
\end{array}} \right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4-3)
$$
在本移动机器人平台中,机器人的运动是处于平面上的,根据机器人运动学可以将式(4-3)化简为(4-4),其中和表示机器人坐标系平面内移动的速度分量,表示围绕机器人中心点平面内旋转的角速度。
$$
\left[ {\begin{array}{*{20}{c}}
{{v_{Xi}}}\\
{{v_{Yi}}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
1&0&{ - {l_{iy}}}
\end{array}}\\
{\begin{array}{*{20}{c}}
0&1&{{l_{ix}}}
\end{array}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{v_X}}\\
{{v_Y}}\\
{{\omega _R}}
\end{array}} \right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4-4)
$$
通过关系式(4-2)、(4-3)与(4-4)可以得到移动机器人的变换矩阵。
$$ {}^{{w_i}}{T_{{P_i}}} = \left[ {\begin{array}{*{20}{c}} 0&{\sin {\gamma _i}}\\ {{r_i}}&{\cos {\gamma _i}} \end{array}} \right] ,\: {}^{{P_i}}{T_R} = \left[ {\begin{array}{*{20}{c}} {\cos {\beta _i}}&{ - \sin {\beta _i}}\\ {\sin {\beta _i}}&{\cos {\beta _i}} \end{array}} \right] ,\: T' = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1&0&{ - {l_{iy}}} \end{array}}\\ {\begin{array}{*{20}{c}} 0&1&{{l_{ix}}} \end{array}} \end{array}} \right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4-5) $$ $$ {r_i} \ne 0,\:0 < |{\gamma _i}| < \frac{\pi }{2},\:\det ({}^{{P_i}}{T_R}) \ne 0,\:\det ({}^{{w_i}}{T_{{P_i}}}) \ne 0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4-6) $$当公式(4-6)成立时,可以得到矩阵变换关系式(4-7)。
$$
\left[ {\begin{array}{*{20}{c}}
{{\omega _i}}\\
{{v_{ir}}}
\end{array}} \right] = {}^{{w_i}}{T_{{P_i}}}^{ - 1} \cdot {}^{{P_i}}{T_R}^{ - 1} \cdot T'\left[ {\begin{array}{*{20}{c}}
{{v_X}}\\
{{v_Y}}\\
{{\omega _R}}
\end{array}} \right],\:i = 1,2,3,4.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4-7)
$$
在移动机器人平台的设计中,四个轮子的半径是一致的,可以用来表示四个轮子的半径,经过整理可得关系式(4-8)。
$$
\left[ {\begin{array}{*{20}{c}}
{{\omega _1}}\\
{{\omega _2}}\\
{{\omega _3}}\\
{{\omega _4}}
\end{array}} \right] = \frac{{ - 1}}{r}\left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{\frac{{\cos ({\beta _1} - {\gamma _1})}}{{\sin {\gamma _1}}}}\\
{\frac{{\cos ({\beta _2} - {\gamma _2})}}{{\sin {\gamma _2}}}}\\
{\frac{{\cos ({\beta _3} - {\gamma _3})}}{{\sin {\gamma _3}}}}\\
{\frac{{\cos ({\beta _4} - {\gamma _4})}}{{\sin {\gamma _4}}}}
\end{array}}&{\begin{array}{*{20}{c}}
{\frac{{sin({\beta _1} - {\gamma _1})}}{{\sin {\gamma _1}}}}\\
{\frac{{sin({\beta _2} - {\gamma _2})}}{{\sin {\gamma _2}}}}\\
{\frac{{sin({\beta _3} - {\gamma _3})}}{{\sin {\gamma _3}}}}\\
{\frac{{sin({\beta _4} - {\gamma _4})}}{{\sin {\gamma _4}}}}
\end{array}}&{\begin{array}{*{20}{c}}
{\frac{{{l_1}sin({\beta _1} - {\gamma _1} - {\alpha _1})}}{{\sin {\gamma _1}}}}\\
{\frac{{{l_2}sin({\beta _2} - {\gamma _2} - {\alpha _2})}}{{\sin {\gamma _2}}}}\\
{\frac{{{l_3}sin({\beta _3} - {\gamma _3} - {\alpha _3})}}{{\sin {\gamma _3}}}}\\
{\frac{{{l_4}sin({\beta _4} - {\gamma _4} - {\alpha _4})}}{{\sin {\gamma _4}}}}
\end{array}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{v_X}}\\
{{v_Y}}\\
{{\omega _R}}
\end{array}} \right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4-8)
$$
3. 通过装配确定最终运动模型
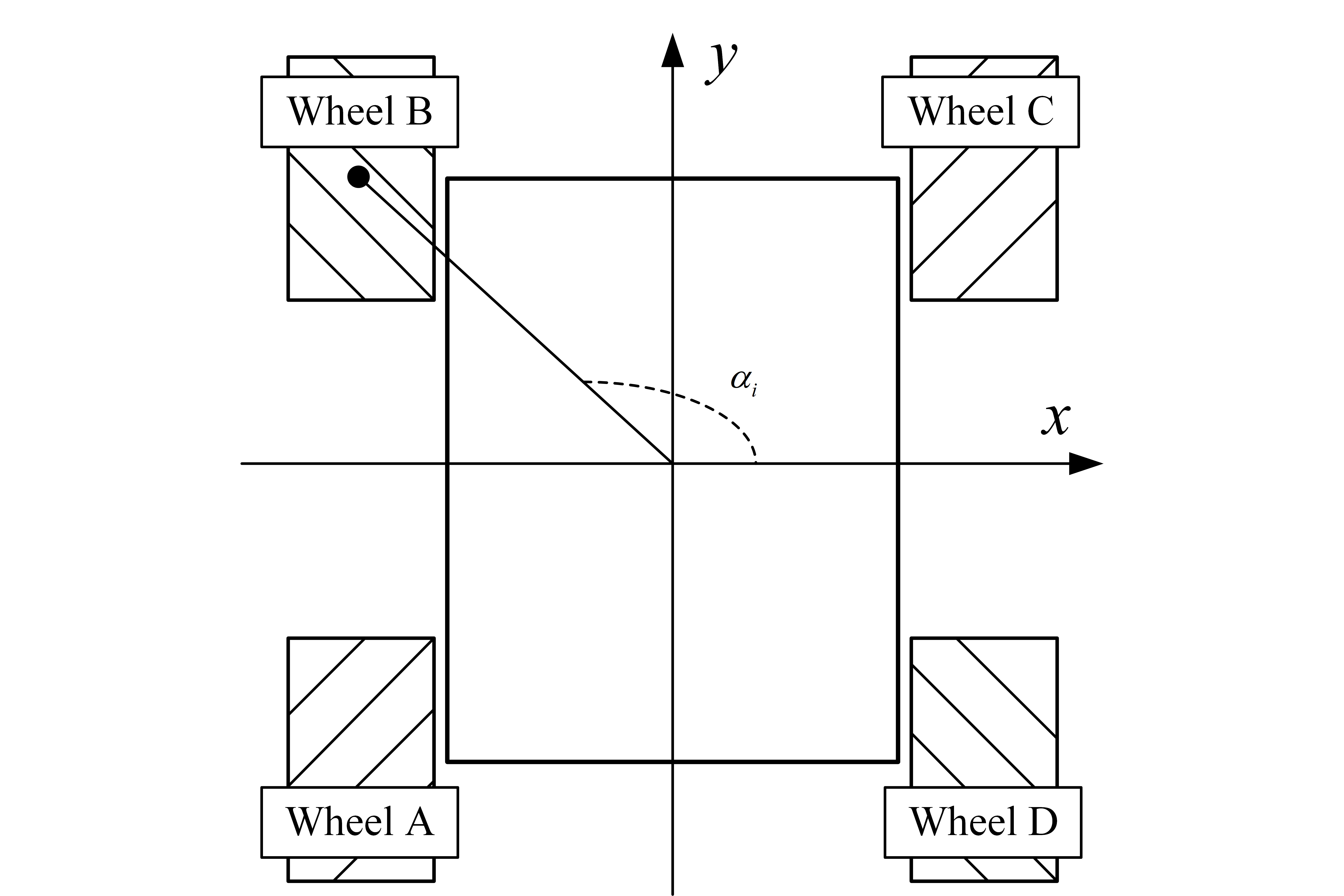
在此给出已经装配好的4-麦克纳姆轮平台的示例,如图3.1所示。
参照图3.1所示移动机器人平台的安装参数,并带入到公式(4-8)中,经过整理最后得到公式(4-9)。
$$
\left[ {\begin{array}{*{20}{c}}
{{\omega _1}}\\
{{\omega _2}}\\
{{\omega _3}}\\
{{\omega _4}}
\end{array}} \right] = \frac{1}{r}\left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
1\\
1\\
1\\
1
\end{array}}&{\begin{array}{*{20}{c}}
{ - 1}\\
1\\
1\\
{ - 1}
\end{array}}&{\begin{array}{*{20}{c}}
{ - ({l_x} + {l_y})}\\
{({l_x} + {l_y})}\\
{ - ({l_x} + {l_y})}\\
{({l_x} + {l_y})}
\end{array}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{v_X}}\\
{{v_Y}}\\
{{\omega _R}}
\end{array}} \right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4-9)
$$
在此设定一个速度矢量,如图3.2所示。其中表示移动平台在X轴上的速度分量,为移动平台在Y轴上的速度分量。
将速度分量与分别代入式(4-10)可得到四个麦克纳姆轮的转速值,因不包含偏航角速度,为零。经过整理可以得到四个麦克纳姆轮的转速,分别用~表示,得到式(4-11)。
$$
\left\{ {\begin{array}{*{20}{c}}
{{v_1} = r{\omega _1} = {v_X} - {v_Y} - ({l_x} + {l_y}){\omega _R}}\\
{{v_2} = r{\omega _2} = {v_X} + {v_Y} + ({l_x} + {l_y}){\omega _R}}\\
{{v_3} = r{\omega _3} = {v_X} + {v_Y} - ({l_x} + {l_y}){\omega _R}}\\
{{v_4} = r{\omega _4} = {v_X} - {v_Y} + ({l_x} + {l_y}){\omega _R}}
\end{array}} \right.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4-10)
$$
通过公式(4-10)对移动机器人平台进行验证即可得到如图3.3所示的平台运动状态,并最终确定建立的机器人移动平台数学模型正确。
参考文献
- Taheri H, Qiao B, Ghaeminezhad N. Kinematic model of a four mecanum wheeled mobile robot[J]. International journal of computer applications, 2015, 113(3): 6-9.
- 孙全胜. 基于STM32单片机的麦克纳姆轮小车设计[J]. 现代信息科技, 2019, 003(022):P.174-175.