【学习手记】MATLAB与机器人仿真项目训练

一、4-DOF MICO串联机器人正逆解

1. 4-DOF MICO串联机器人系统介绍

机器人基本技术参数设计主要是根据设计任务和功能要求，来确定以下主要性能参数:机器人的用途:根据设计要求，所设计的机器人主要用于柔性制造系统中刀具更换、工件运送和装配。机器人的负载能力:机器人末端执行器持重为: 2kg。末端执行器与本体之间以接口的形式连接以便对多种末端执行器进行替换。
传动系统设计是机器人设计过程中最主要的设计问题之一。机器入的传动系统除采用齿轮、蜗轮蜗杆和行星齿轮传动外，还广泛采用滚珠丝杠、谐波减速装置和绳轮钢带等传动装置。如果机器人的成本允许，传动系统应避免自己加工制造，尽可能采用知名厂家成熟的传动产品。传动装置在机器人的设计中是一个很重要的环节，传动的好坏直接影响到最后的控制性能。

随着机器人应用领域的不断扩大，机器人产品也正在向多品种、小批量、低成本等方向发展，这就对机器人本体的设计和生产提出了新的要求。机器人本体的设计应尽可能标准化、模块化以缩短开发和生产周期，降低生产成本。采用模块化设计还可以有效地提高设计的重用性，增加系统的可靠性，并能根据客户需要对系统进行合理配置从而满足市场的不同需求，四自由度串联机器人本体的大臂和小臂关节都是转动关节，用于实现在同一.平面内的定位，而大臂和小臂也具有相似的功能。

由于四自由度串联机器人相当于开链式连杆结构，其臂部关节和末端执行器的结构及重量对机器人整体静、动态性能有较大的影响，从而对机器人的工作效率、稳定性和可靠性有很大影响。因此除采用轻型、高强度铝合金材料外，还应设计重量较轻、刚性较好的机械结构。回转机座又称机器人的腰座，用来实现腰部回转。腰部轴系及传动链的精度和刚度对末端执行器的运动精度影响最大。因此腰座与手臂的连接要有可靠的定位基准面。腰部承受机器人全部重量和工作载荷，应具有足够的强度、刚度和承载能力。而且，为保证机器人工作的稳定性，安装基面要足够大。四自由度串联机器人的升降移动关节用于驱动机器人大臂、小臂作升降直线运动，从而实现末端执行器在垂直方向的运动。常用的直线驱动方式主要有液压驱动、气压驱动、直线电机驱动、旋转电机与丝杠螺母副联合驱动等。因滚珠丝杠螺母具有传动摩擦力矩小、传动效率高、结构紧凑、刚性好、传动精度高、工作寿命长等特点在机电一体化系统中取得了广泛应用。而由滚珠螺杆与线性滑轨构成的精密线性模组具有体积小、重量轻、高精度、高刚性、组装便利、维护容易等优点。目前已广泛应用在精密机械与其它需要精密定位的机构上。

四自由度串联型机器人的运动学模型的建立，包括机器人运动学方程的表示以及运动学正解、逆解等，这些是研究机器人控制的重要基础，也是开放式机器人系统轨迹规划的重要基础。四自由度串联型机器人操作臂可以看作是一个开式运动链。它是由一系列连杆通过转动或移动关节串联而成的。为了研究操作臂各连杆之间的位移关系，可在每个连杆上固接一个坐标系(附体坐标系)，然后描述这些坐标系之间的关系。

2. 正解

（1）原理

机械臂一般是由关节和连杆构成的。各关节均是可以旋转的，是线性滑动的。每一个关节都被定义为一个自由度 (DOF) 。在这个实验中，我们定义这是一个有四个可旋转的关节的四自由度机械臂。对机械臂连杆进行编号，从已固定的底座到最末端的机械臂连杆分别为${L_0}$、${L_1}$、${L_2}$、${L_3}$。

图1.2.1连杆坐标系示意图
机械臂的各个关节都有一个旋转的轴(由${Z_i}$表示，其中$i$表示关节的编号)，称为关节轴。

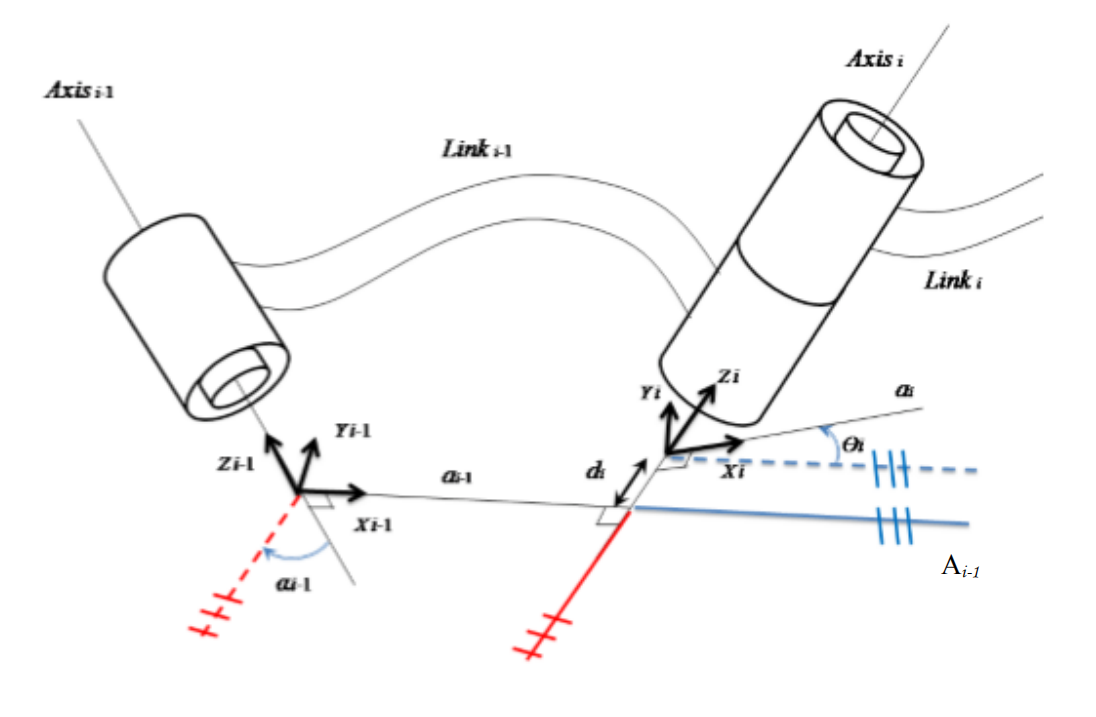
机械臂的每个连杆都’可看作’是-个用来定义两个相邻关节轴之间关系的刚体。参考图1.2.1中的两个相邻关节坐标系。为了确定两个固定轴(固定不动)的相对位置和方向，仅需要两个参数:连杆长度和连杆扭角。

连杆长度${a{i - 1}}$:两相邻关节$i - 1$和$i$的关节轴之间的距离(${a{i - 1}}$ 所在直线垂直于关节$i - 1$和$i$的关节轴，即公共法线$Axi{s_{i - 1}}$)。

连杆扭角${\alpha {i - 1}}$ :两相邻关节$i - 1$和$i$的关节轴之间的夹角角度(若两轴相互平行，则${\alpha {i - 1}} = 0$)。

如果考虑附加轴(3个或更多固定轴)，通常情况下，公共法线不会同时与公共轴相交。因此，需要一个新的参数来描述相邻关节轴之间的关系，即连杆偏移。

连杆偏移${di}$:关节轴$i$相对于关节轴$i - 1$和$i + 1$的两条公共法线$Axi{s {i - 1}}$和$Axi{s _i}$之间的距离。

如果所有的轴都是不固定的，则还需要最后一个参数来描述相邻关节轴之间的关系，即关节角度。

关节角度${\theta i}$：关于关节轴$i$的公共法线$Axi{s {i - 1}}$和$Axi{s _i}$之间的夹角角度。

这四个参数(${a{i - 1}}$、${\alpha {i - 1}}$、${d_i}$和${\theta _i}$)是机器人的Denavit-Hartenberg或DH参数。

如前所述，为了描述每个连杆相对于其相邻连杆的位置和方向，每个连杆上都建立了一个坐标系。我们假设所有的关节都是原点，则${x_0}$轴指向机器人的前方, ${y_0}$轴指向左侧，${z_0}$轴指向上方(与关节轴对齐)。

根据以下步骤给机械臂的连杆建立坐标系：

1、给每个连杆$i$指定一个坐标系$i$;

2、${z_i}$轴就是关节轴(可旋转);

3、选择关节轴和公共法线$Axi{s i}$的交点(或者若${\alpha {i - 1}} = 0$，则选择关节轴$i$和$i + 1$的交点)作为坐标系$i$的原点;

4、${xi}$轴沿着公共法线$Axi{s_i}$，指向关节$i+1$。如果${\alpha{i - 1}} = 0$，则${xi}$轴垂直于${z_i}$轴和${z{i + 1}}$轴且方向任意:若${\thetai} = 0$，则最好沿着${x{i - 1}}$轴选择;

5、${y_i}$轴通过右手法则来确定。

根据上述步骤建立的坐标系,${a{i - 1}}$是${z{i - 1}}$轴和${zi}$轴之间的距离(沿${x{i - 1}}$轴方向),${\alpha{i - 1}}$是${z{i - 1}}$轴和${zi}$轴之间夹角的角度(关于${x{i - 1}}$轴)，${di}$是${x{i - 1}}$轴和${xi}$轴之间的距离(沿${z_i}$轴方向),${\theta_i}$是${x{i - 1}}$轴和${x_i}$轴之间夹角的角度(关于${z_i}$轴)。
将机械臂连杆所对应的坐标系相关的旋转和平移矩阵相乘后(这两个变换矩阵对应的是两个相邻坐标系$i$和$i - 1$,且使用了已定义的DH参数)，其中$c$与$s$分别代表$sin$与$cos$,所得关系为:

T = [\begin{matrix} c θ_{i} & - s θ_{i} & 0 & α_{i - 1} \\ s θ_{i} c α_{i - 1} & c θ_{i} c α_{i - 1} & - s α_{i - 1} & - s α_{i - 1} d_{i} \\ s θ_{i} s α_{i - 1} & c θ_{i} s α_{i - 1} & c α_{i - 1} & s α_{i - 1} d_{i} \\ 0 & 0 & 0 & 1 \end{matrix}]

(2) Matlab仿真

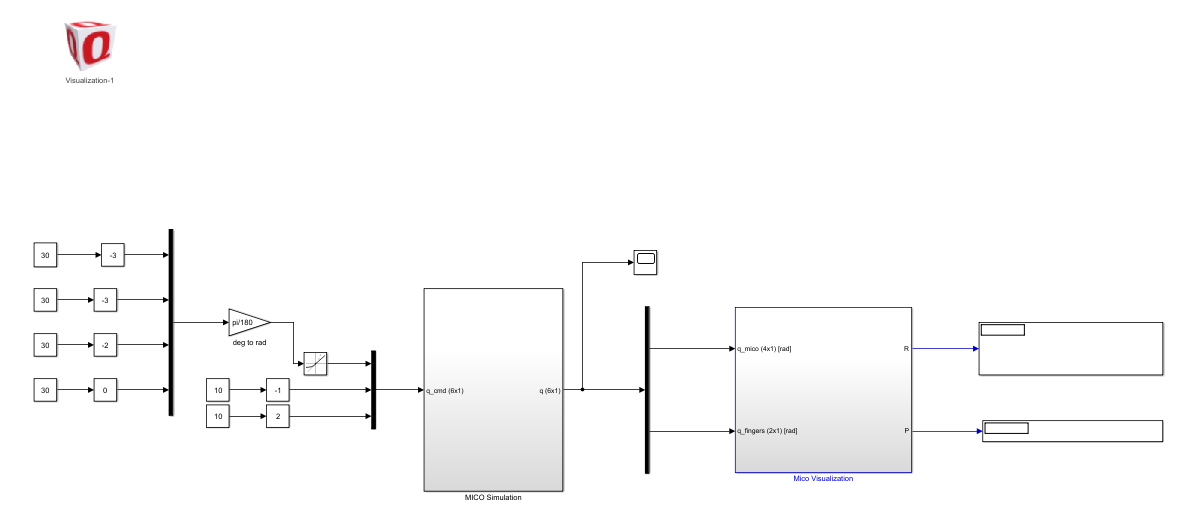
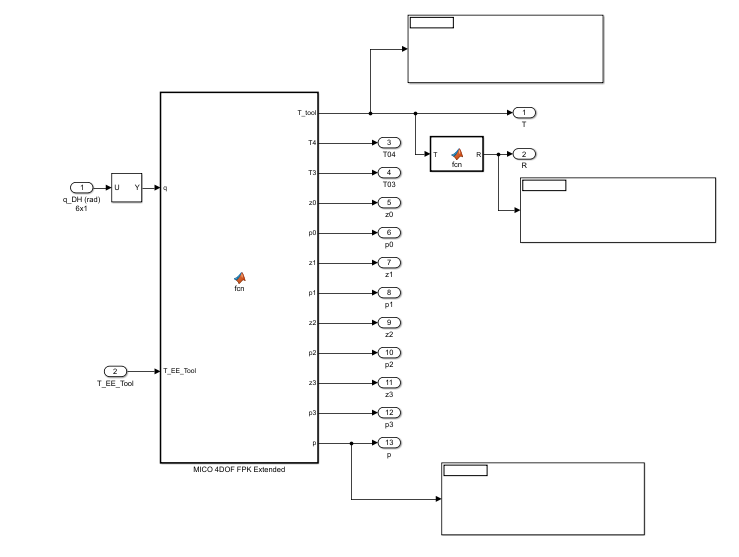
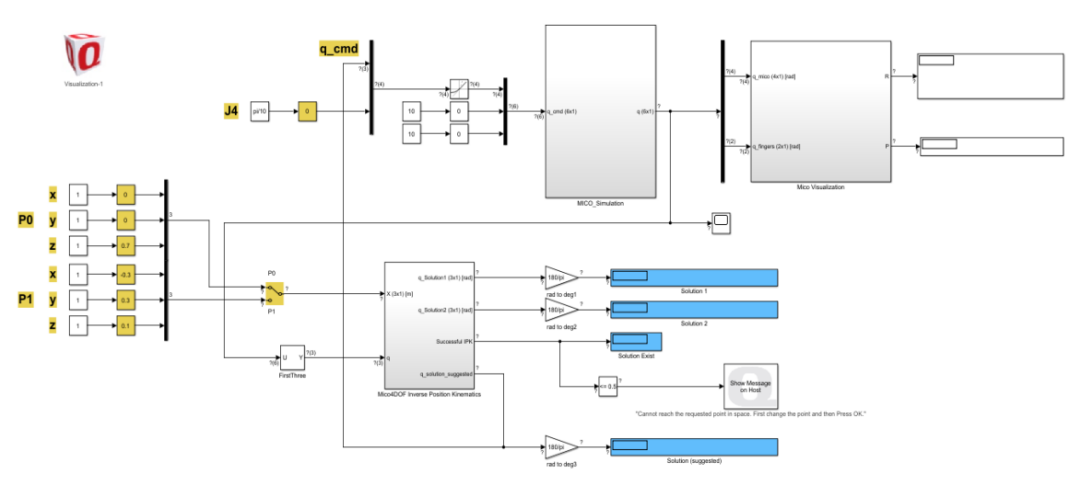
首先编写DH.m程序（程序见附录），FPK程序同，打开simulation仿真模型。
图1.2.2 系统simulation仿真模型
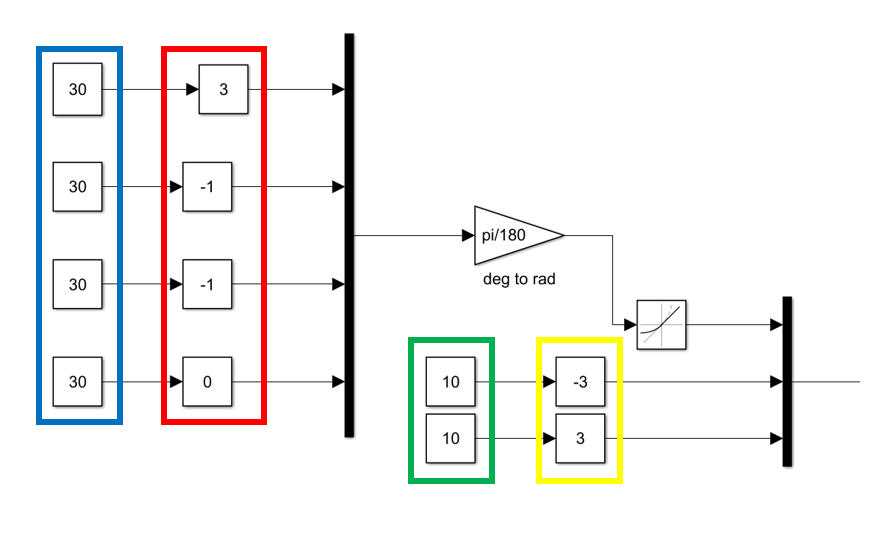
在FPK模块输出加入几个示波器矩阵。
图1.2.3 FPK模块示意图
对系统进行仿真。点击simulation菜单栏的QUARC下拉菜单Build。
图1.2.4 QUARC build选项菜单
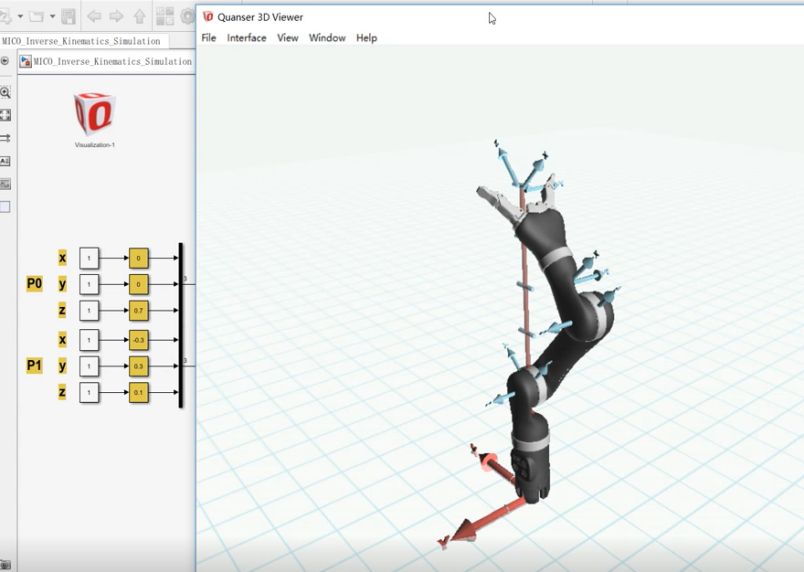
完成后点击连接即可打开Quarc3D图像。
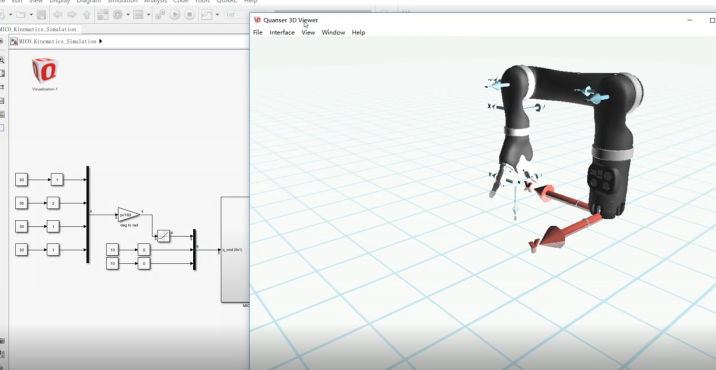
图1.2.5 Quarc3D机械臂图像
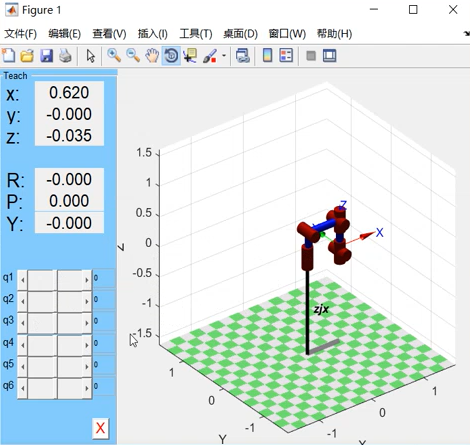
点击运行。输出如下：
图1.2.6 输出参数矩阵
修改左边输入角度参数即可改变机器人的位姿。
图1.2.7 机器人输入参数
图1.2.8 修改参数后机器人图
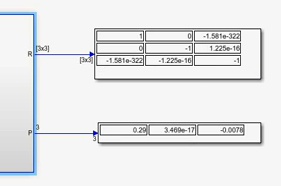
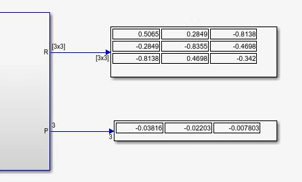
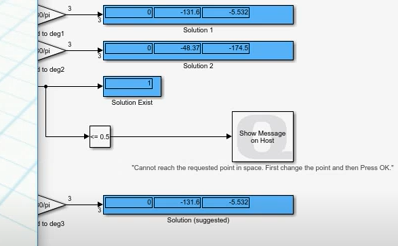
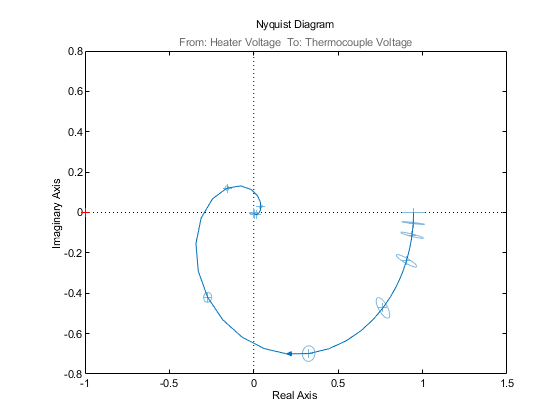
输出参数矩阵如下：
图1.2.9 修改后机器人输出参数
小结：根据图1.2.6可以看出，输出与输入存在些许误差。可能是由于模型系统本身造成的。

3. 逆解

（1）原理

一般来说，机械臂运动学方程的求解是一个非线性、重要的问题。机械臂的末端执行器的坐标可通过其4x4的转换矩阵来表示。其中有四个元素是固定的(变换矩阵的最后一行是[0001] )，变换矩阵的其余12 个元素被分为一个3x1的位置向量和3x3的方向矩阵。另外，旋转矩阵中的9个参数不是独立的。一个坐标系相对于另一个坐标系的方向可用3个独立的参数来表示，这三个参数分别被称为roll(滚动,绕x轴旋转),pitch (俯仰，绕y轴旋转)，yaw (偏航，绕z轴旋转)。

为了完成指定的空间姿态(x，y, z，toll, pitch, yaw)，这六个关节变量是必不可少的。因此，在使用4自由的机械臂时，其末端执行器无法按照指定的方向到达空间中的每个位置。也可以说4自由度机械臂没有灵活的工作空间，或者说没有一个可以使得末端执行器能够到达任意位置的空间量。可到达工作空间指的是机器人末端执行器至少一个方向可以到达的空间量。

对于4-DOF MICO机械臂，由于第一个关节可以移动360°，因此可以到达的工作空间为： $({x^2} + {y^2} + {(z - ({L_0} + {L_1}))^2}) \le {L_2} + {L_3} + {L_4}$ 需要注意${x^2} + {y^2} + {(z - ({L_0} + {L_1}))^2}$为末端执行器与坐标系J2 (关节2)的原点间的距离。如果这个距离大于连杆2, 3和4的长度和，则机械臂无法到达这个位置。因此，只要是满足上述不等式空间的所有点，且产生的关节角度不超过物理限制，我们都可以得到一个对应的解。对于4-DOF MICO机械臂,关节2的角度限制为$ - {220^ \circ } < {\theta _2} < {40^ \circ }$,关节3的角度限制为$ - {230^ \circ } < {\theta _3} < {50^ \circ }$。

在本实验中，我们对机械臂末端执行器不同位置可能对应的关节位置进行了求解，并研究了可能的方向。机械臂末端执行器所需的三个变量:$x$，$y$和$z$。查看图1.3.1中的机械臂示意图(侧视图)，机械臂最后一个关节(J)的变化不会影响末端执行器的位置，只会改变末端执行器的方向。所以，最终我们只需要求解已给定$x$，$y$和$z$的前三个关节角度(${\theta_1}$，${\theta_2}$和${\theta_3}$)。
图1.3.1 4-DOF MICO机械臂的2D侧视图和俯视图
机器人逆向运动学的解法有两种:数值解法和封闭解法。数值解法会给出关节变量的具体数值。封闭算法是使用代数方程或几何计算得到的表达式。在这里我们提供了使用几何计算的封闭算法解决方案。

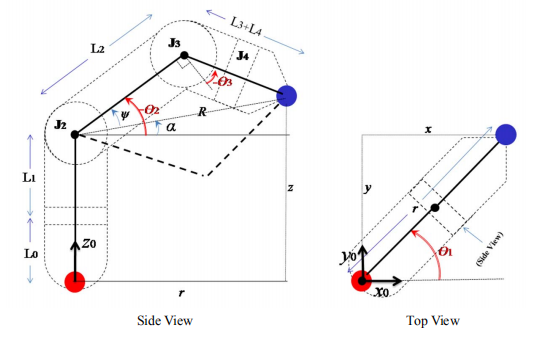
逆向运动学的几何解法是-一种直接且简单的算法，用于求解给定的末端执行器位置所对应的关节角度。在这个算法中，我们尝试将机械臂的空间几何分解为简单的平面几何问题。当第一个关节(J1)改变时，4-DOF MICO机械臂的运动可以被分解为一个移动的平面，该平面绕z轴旋转。图1.3.1中是机械臂的两个不同视角下的平面图。左图是移动平面的侧视图，右图是俯视图。

根据图1.3.1中的侧视图，可以推导出$r$和$z$,如下所示:

$r = ({L_2}cos({\theta _2})) - ({L_3} + {L_4})sin({\theta _2} + {\theta _3}))$$$$z = {L_0} + {L_1} - {L_2}\sin ({\theta _2}) - ({L_3} + {L_4})cos({\theta _2} + {\theta _3})$

根据图1.3.1中的俯视图，可以推导出$x$和$y$，如下所示:

$x = r\cos ({\theta _1})$$$$y = r\sin ({\theta _1})$

根据上述几个式子可知：

${\theta _1} = a\tan 2(x.y)$

另外，根据图1.3.1中的侧视图还可以，推导出：

R = \sqrt{r^{2} + {(z - (L_{0} + L_{1}))}^{2}}

要计算关节角${\theta_2}$和${\theta_3}$，首先要计算$\alpha $和$\psi $，可以使用以下公式来计算角度$\alpha $:

α = \tan^{- 1} (z - (L_{0} + L_{1}), r) = t a n^{- 1} \frac{z - (L_{0} + L_{1})}{\sqrt{x^{2} + y^{2}}}

其中，${\tan ^{ - 1}}$是用atan2命令来计算的。给定了$x$,$y$和$z$,要计算$\psi $,需要使用余弦定理。余弦定理，也成为余弦公式或余弦法则，表示了三角形的边长和其中一个角度的余弦之间的关系，如图1.3.2所示，其中${c^2} = {a^2} + {b^2} - 2ab\cos \gamma $。 ![图1.3.2 余弦定理](1.3.2.png) 将余弦定理应用到由$R$，${L_2}$，${L_3}+{L_4}$和角度$\psi $表示的三角形上，可以得到:

{(L_{3} + L_{4})}^{2} = R^{2} + L^{2} - 2 L_{2} R \cos ψ \Rightarrow ψ = \cos^{- 1} (\frac{R^{2} + L^{2}_{2} - (L_{3} + L_{4})}{2 L_{2} R})

其中R参考公式:

R = \sqrt{r^{2} + {(z - (L_{0} + L_{1}))}^{2}}

同样的，将余弦定理应用到由$R$，${L_2}$，${L_3} + {L_4}$和角度$\frac{\pi }{2} - {\theta _3}$表示的三角形上，可以得到：

θ_{3} = \sin^{- 1} (\frac{L^{2}_{2} + (L_{3} + L_{4}) - (x^{2} + y^{2} + {(z - (L_{0} + L_{1}))}^{2})}{2 L_{2} (L_{3} + L_{4})})

现在，根据图1.3.1可以得到以下两组关节角度的解，第一组解：

θ_{1} = \tan^{- 1} (\frac{y}{x})

θ_{2} = - (α + ψ)

θ_{3} = \sin^{- 1} (\frac{L^{2}_{2} + (L_{3} + L_{4}) - (x^{2} + y^{2} + {(z - (L_{0} + L_{1}))}^{2})}{2 L_{2} (L_{3} + L_{4})})

第二组解：

θ_{1} = \tan^{- 1} (\frac{y}{x})

θ_{2} = - (α - ψ)

θ_{3} = - π - \sin^{- 1} (\frac{L^{2}_{2} + (L_{3} + L_{4}) - (x^{2} + y^{2} + {(z - (L_{0} + L_{1}))}^{2})}{2 L_{2} (L_{3} + L_{4})})

(2) Matlab仿真

首先编写DH.m程序（程序见附录），FPK程序同，打开simulation仿真模型。
图1.3.3 系统simulation仿真模型
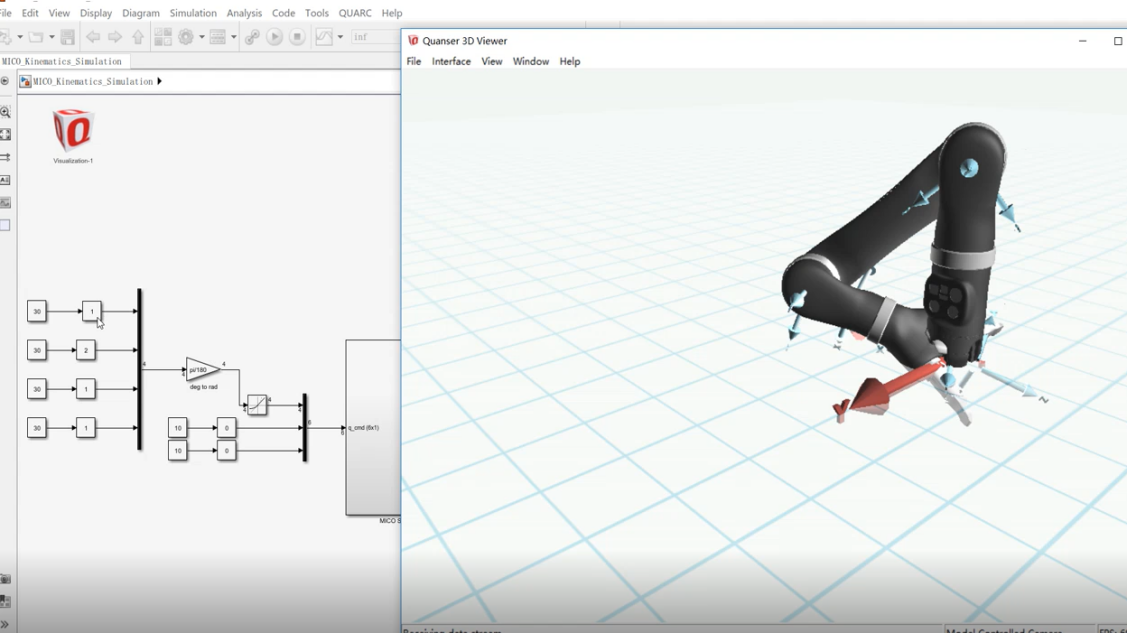
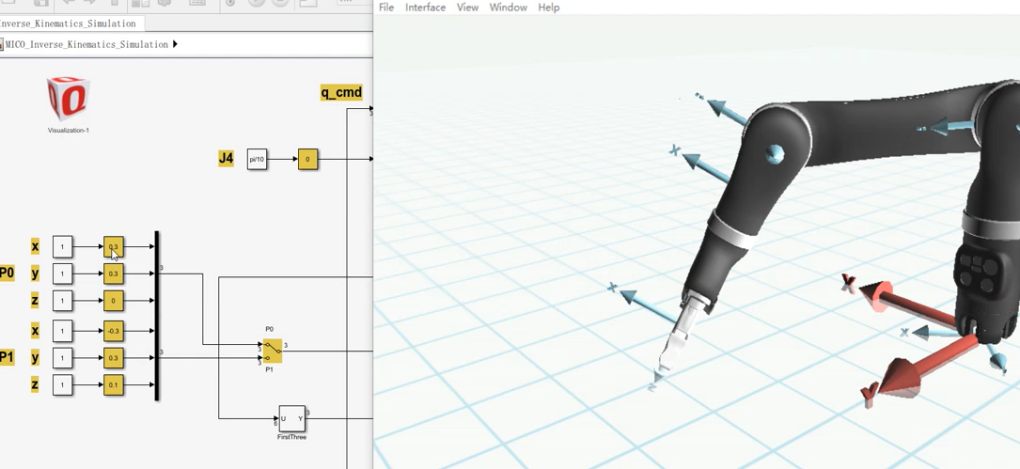
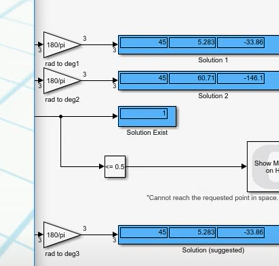
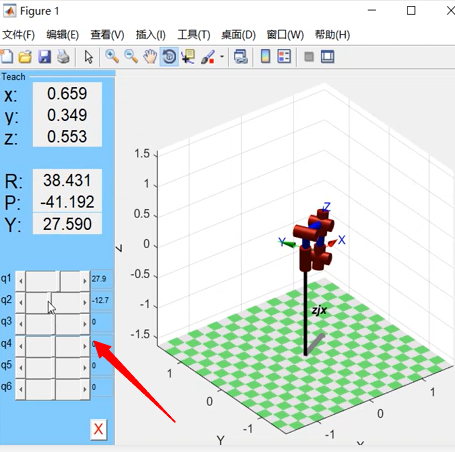
对系统进行仿真。点击simulation菜单栏的QUARC下拉菜单Build。完成后点击连接即可打开Quarc3D图像，将输入打到P1，点击运行。
图1.3.4 Quarc仿真图像
图1.3.5 输出参数矩阵
修改左边输入角度参数即可改变机器人的位姿。$x = 0.3$，$y = 0.3$，$z = 0$。
图1.3.6 修改后机器人位姿示意图
图1.3.7 修改机器人输出参数
小结：机器人逆解模型就是在正解的基础上加上逆解程序，机器人的逆解输出也用于正解。逆解存在两个输入类型，可以在P0、P1之间切换。

二、机械臂逆解算法改进与仿真

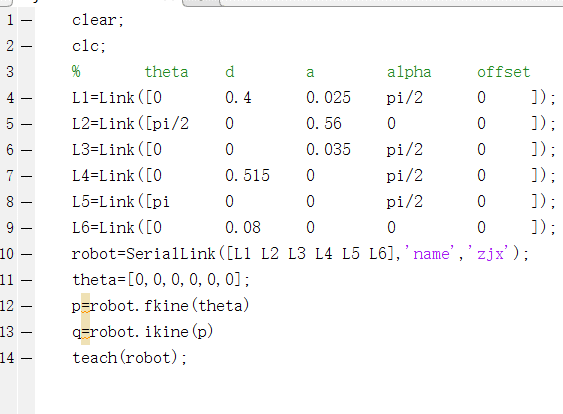
根据任务要求查阅资料我们决定使用机器人工具包进行逆解算法的改进工作。我们使用Link函数对机器人的各个参数进行程序的编写。其中，p为机器人的位姿，q为机器人输出的关节角。
图2.1.1 逆解优化程序
新建Matlab的m文件输入上图的程序并运行。
图2.1.2 机器人位姿示意图
图2.1.3 修改关节角度
小结：逆解优化使用机器人工具箱可以对机器人的关节角进行修改，操作相对于Quarc来说更加简便，总体来说优化任务圆满完成，实现对机械臂的便捷控制。

三、项目总结

在大多数的机器人应用中，机器人末端执行器需要能够到达空间中一个特定的已知位置和方向，从而完成特定的任务。反向运动学解决了末端执行器为了放置到一个特定的位置而所需要的关节角度的问题。机械臂是通过模仿人的手和臂的设计进行自动操作装置，可以实现对物体的搬运、抓取等任务。它可以在恶劣的环境或是人类无法工作的情况下，代替人进行作业。因此，机械臂被广泛应用于机械制造、医疗、冶金、电子、航空航天和原子能等领域。机械臂的逆运动学问题是一个比较繁琐的过程，其求解的速度和精度能直接影响到机械臂控制的精度。因此，对机械臂的逆运动学的研究主要集中在解的存在性与逆解算法上。机械臂逆运动学的求解方法主要有:迭代法、解析法和几何法。

四自由度关节式机器人为研究对象通过经典D-H法对其进行运动学分析,并用MATLAB进行了运动学的仿真与方程计算，通过数据对比分析验证了运动学模型与运动学正逆运算的正确性。为机器人进行轨迹规划研究与仿真提供了必要的理论基础和正确的运动学模型。多关节串联机器人的逆运动学优化计算问题，在机器人学科领域,与之密切相关的技术问题包括：机械臂的轨迹规划技术，人机交互式操作控制技术,机械臂视觉伺服控制技术以及计算机虚拟现实技术等。介绍了于求解串联机器人逆运动学问题的主要数值计算方法,研究了串联机器人的结构参数建模问题,在此基础上,得到空间坐标系下机器人的位置和姿态矩阵,以及描述机器人运动关系的旋转变换矩阵。进一步得建立了以位置和姿态误差量表示的关于n-1关节串联机器人的逆运动学问题的目标函数。