1. 已知电机基本参数

我们需要以下数据：
其中电机额定电压，额定电流，电机电阻，电机电感，
额定转速，电机模型转动惯量（本人学号尾数为9通过要求计算得到）；PWM放大器时间常数，PWM放大倍数，并已知速度反馈系数。

2. 电机模型计算

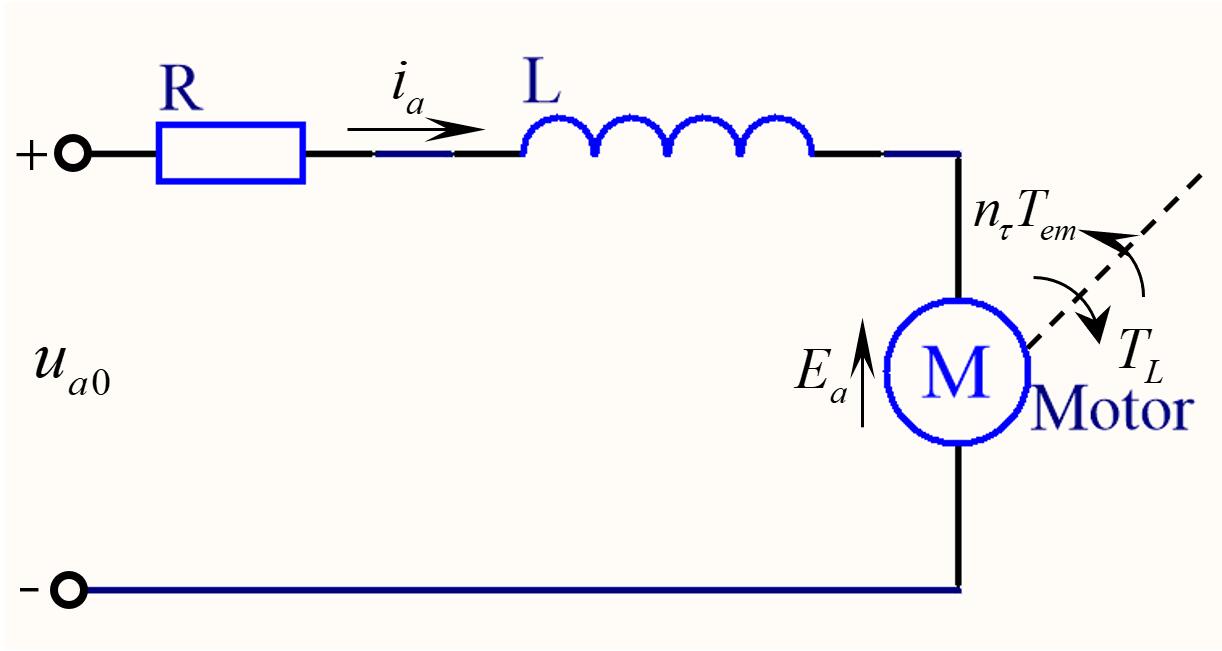
知道有关直流电机参数后可以进行电机的建模，首先可以将直流电机简化为图2.1的电路模型：

图2.1 直流电机简化电路模型

由简化的电路模型可以得出以下表达式，基尔霍夫定律，直流电机电路模型：

$$ {u_{a0}} = R{i_a} + L\frac{{d{i_a}}}{{dt}} + {E_a} $$

额定励磁下的感应电动势：
$${E_a} = {C_e}n$$
根据牛顿动力学定律，忽略空载转矩：
$${T_{em}} = {T_L} + \frac{{G{D^2}}}{{375}}\frac{{dn}}{{dt}}$$
额定励磁下的电磁转矩：

$${T_{em}} = {C_T}{i_a}$$

额定励磁下的转矩电流比：
$${C_T} = \frac{{30}}{\pi }{C_e}$$
其中，为电机的负载转矩，即外界施加的负载，单位为牛米（）； 为电力拖动系统运动部分折算到电动机轴上的飞轮力矩，其中可以与电机模型转动惯量等价，单位为牛米方（）；为转矩电流比，单位为； 为电动势常数，单位为。
在额定条件下，只考虑电阻影响，可以求出的大小：
$${C_e} = \frac{{{U_N} - R{I_N}}}{{{n_N}}} = 1.3 \times {10^{ - 3}}V \cdot \min /r$$
在进行永磁式直流电机建模时需要计算并求取其传递函数，因此分别进行时间常数的定义。定义电枢回路电磁时间常数为，定义电力拖动系统的机电时间常数为并列出以下方程：
$${T_a} = \frac{L}{R}$$

$${T_m} = \frac{{G{D^2}R}}{{375{C_e}{C_T}}}$$

输入转矩与负载电流之间的关系可以表示为：
$${i_{aL}} = \frac{{{T_L}}}{{{C_T}}}$$
将 、、方程带入电机的模型方程可以得出以下微分方程,电压电流间传递函数：
$$\frac{{{I_a}(s)}}{{{U_{a0}}(s) - {E_a}(s)}} = \frac{{1/R}}{{{T_a}s + 1}}$$
电流与电动势间传递函数：
$$\frac{{{E_a}(s)}}{{{I_a}(s) - {I_{aL}}(s)}} = \frac{R}{{{T_m}s}}$$
负载转矩与负载电流间传递函数：
$$\frac{{{T_L}(s)}}{{{I_{aL}}(s)}} = \frac{1}{{{C_T}}}$$
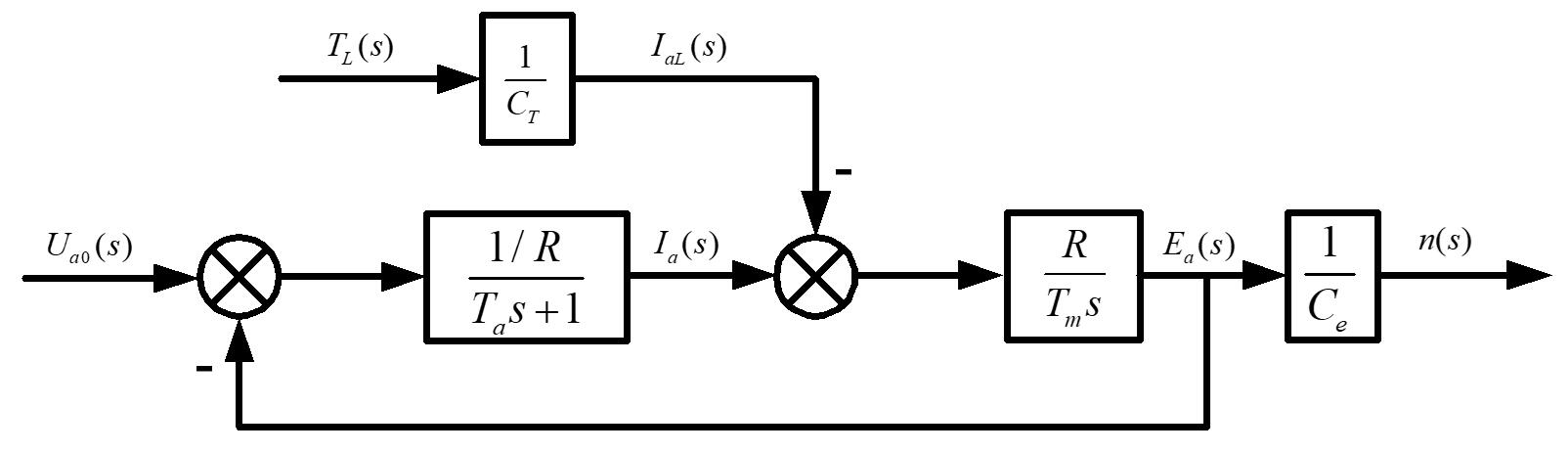
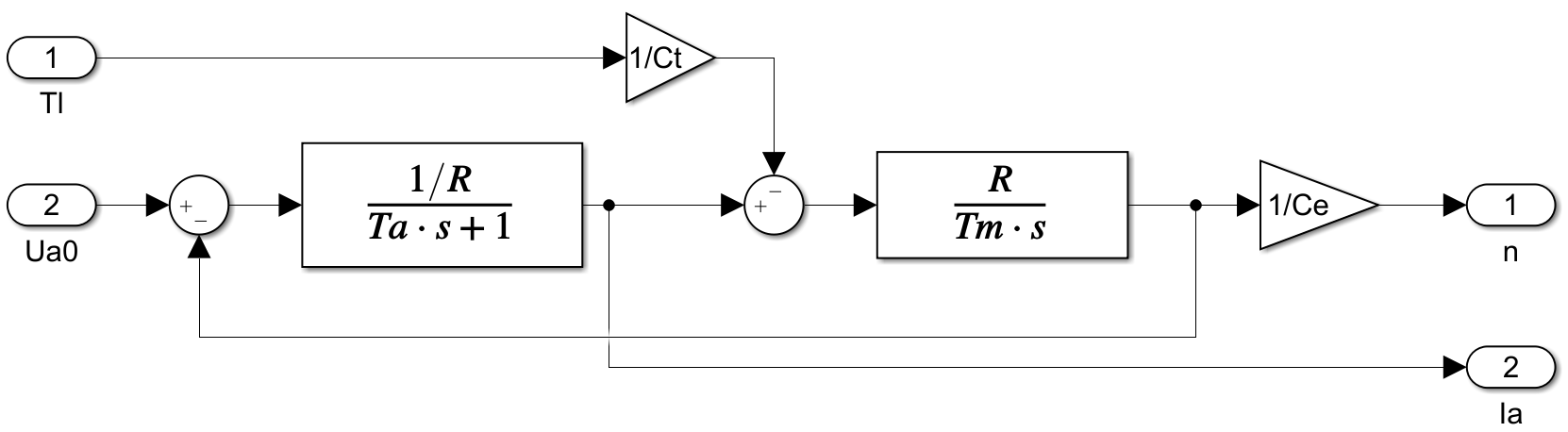
通过传递函数的整理可得直流电机的动态结构图如图2.2所示：

图2.2 永磁直流电机动态结构图

经过整理可得传递函数为(理想空载条件下.)：
$$\frac{{{U_{a0}}(s)}}{{n(s)}} = \frac{{1/{C_e}}}{{{T_m}{T_a}{s^2} + {T_m}s + 1}} = \frac{{775.8433}}{{0.0595{s^2} + 0.9314s + 1}}$$

3. 仿真系统的传递函数

单闭环永磁直流电机控制系统主要包括三个子系统，分别为永磁式直流电机、PWM脉宽调节器和PID控制器。以下为PWM脉宽调节器与PID控制器的传递函数构建，电机已经在电机建模计算中进行详细的传递函数搭建，因此不再赘述。

（1）PWM脉宽调节器的模型搭建：

PWM脉宽调节器主要由脉宽调制器、驱动电路、变换器构成。当输入的控制电压改变时，变换器的输出电压需要下一周期才能发生改变，因此可以将三者进行简化计算，共同看成一个滞后环节。因此PWM脉宽调节器的传递函数可以简化为：

$$\frac{{{U_{a0}}(s)}}{{{U_{ct}}(s)}} = {K_s}{e^{ - {T_s}s}}$$

因为此传递函数中包含指数，所以系统为非最小相位系统，进行分析以及计算都非常麻烦，需要进行近似计算。先用泰勒级数将进行展开：

$$\frac{{{U_{a0}}(s)}}{{{U_{ct}}(s)}} = \frac{{{K_s}}}{{1 + {T_s}s + \frac{1}{{2!}}T_s^2{s^2} + \frac{1}{{3!}}T_s^3{s^3} + \cdots }}$$

考虑到非常小，忽略其高次项，则PWM脉宽调节装置的传递函数可近似成一阶惯性环节，其传递函数为：

$$\frac{{{U_{a0}}(s)}}{{{U_{ct}}(s)}} \approx \frac{{{K_s}}}{{{T_s}s + 1}}$$

根据传递函数，只要传递函数就成立；依照自控原理的相关知识，将转换为，便得到相应的幅相频率特性，经过化简，得到的传递函数成立条件为：

$$\frac{1}{{2!}}T_s^2{\omega ^2} \ll 1$$

推广到工程上，只要满足远小于0.1就可以认为上式成立，所以得到系统的传递函数为：

$$\frac{{{U_{a0}}(s)}}{{{U_{ct}}(s)}} = \frac{{{K_s}}}{{{T_s}s + 1}},\frac{1}{{2!}}T_s^2{\omega ^2} \ll 0.1$$

（2） PID控制器的模型搭建：

PID控制器是按偏差的比例（Proportion）、积分（Integration）、微分（Differentiation）进行控制的调节器简称，它主要针对控制对象来进行参数调节。在本次报告中主要进行PI控制器与PID控制器的讨论。

PI控制器：比例积分控制器通过比例环节与积分环节进行调节，P作用的输出与偏差成比例，称为比例控制作用；I作用的输出与偏差的积分成比例，称为积分控制作用。

其输出与偏差的关系为：

$$u(t) = {K_p}[e(t) + \frac{1}{{{T_I}}}\int {e(t)dt]}$$

设：

因此PI控制器所对应的开环传递函数为：

$$\frac{{{U_{ct}}(s)}}{{\Delta {U_n}(s)}} = {K_p} + {K_i}\frac{1}{s}$$

其中为比例放大系数，为积分时间常数。

PID控制器：比例积分微分控制器在PI控制器的基础上增加了微分环节，在PI作用的基础上增加D作用的输出与偏差的微分成比例，称为微分控制作用。其输出与偏差关系为：

$$u(t) = {K_p}e(t) + {K_i}\int_0^1 {e(t)dt} + {K_d}\frac{{de(t)}}{{dt}}$$ $${K_d} = {T_D}{K_p}$$

对u(t)求拉普拉斯变换并且整理可得PID控制器的开环传递函数为：

$$\frac{{{U_{ct}}(s)}}{{\Delta {U_n}(s)}} = \frac{{{K_p}(s + {K_d}{s^2} + {K_i})}}{{s{{(s + 1)}^2}}}$$

式中的为微分时间常数。

因为采用两种不同的控制器，因此单闭环直流电机控制系统的模型也不相同，于是分别求两个不同控制器系统的传递函数与动态结构图。本单闭环系统主要以检测电机的转速并且将电机的转速转换为相应的电压并与输入的电压进行比较。

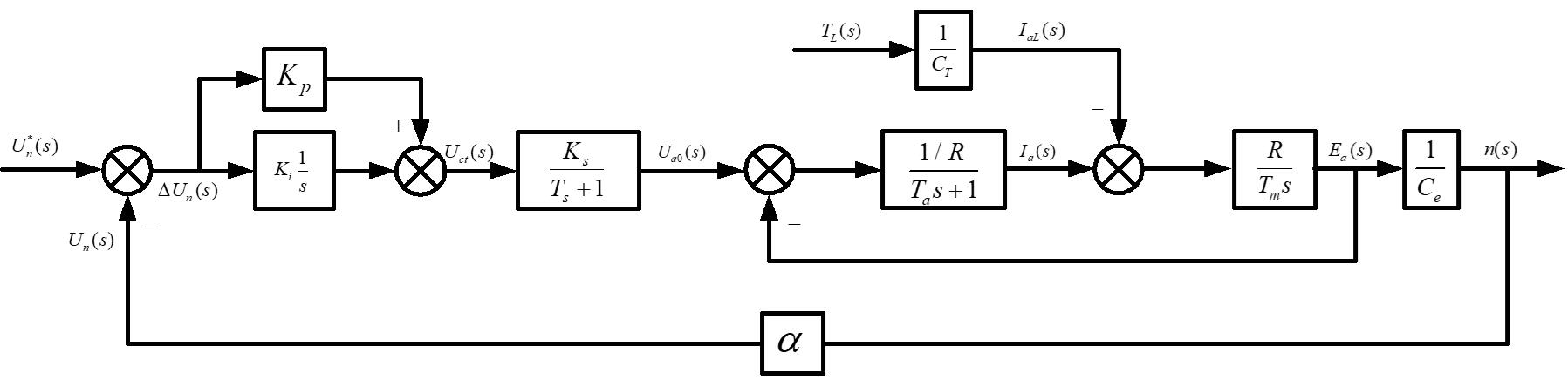
以PI控制器的单闭环直流电机控制系统传递函数模型如图3.1所示，已知各个环节的传递函数可以求出传递函数。

图3.1 单闭环直流调速系统动态图（PI）

以PI控制器的单闭环直流调速系统传递函数推导可先求出整个系统的开环传递函数，用表示，则开环传递函数如下（理想空载条件下）：

$${G_{pi}}(s) = \frac{{{K_p}{K_s}s + {K_i}{K_s}}}{{{C_e}{T_a}{T_m}{T_s}{s^4} + ({C_e}{T_a}{T_m} + {C_e}{T_m}{T_s}){s^3} + ({C_e}{T_m} + {C_e}{T_s}){s^2} + {C_e}s}}$$

则闭环传递函数为：

$${\Phi _{pi}}(s) = \frac{{{G_{pi}}}}{{1 + {G_{pi}}\alpha }} = \frac{{{K_p}{K_s}s + {K_i}{K_s}}}{{{C_e}{T_a}{T_m}{T_s}{s^4} + {C_e}{T_m}({T_a} + {T_s}){s^3} + {C_e}({T_m} + {T_s}){s^2} + ({C_e} + \alpha {K_p}{K_s})s + \alpha {K_i}{K_s}}}$$

设、都为1，并且代入已知参数可以得到系统的闭环传递函数为：

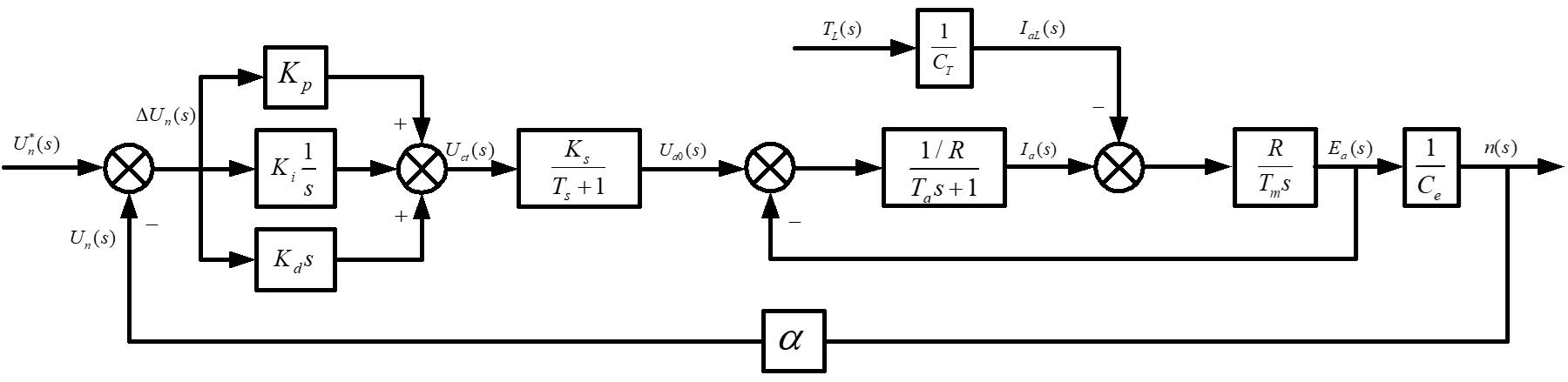
$${\Phi _{pi}}(s) = \frac{{5s + 5}}{{7.6754 \times {{10}^{ - 9}}{s^4} + 7.6874 \times {{10}^{ - 5}}{s^3} + 0.0012{s^2} + 0.0163s + 0.015}}$$

以PID控制器的单闭环直流电机控制系统传递函数模型如图3.2所示，已知各个环节的传递函数可以求出传递函数。

图3.2 单闭环直流调速系统动态图（PID）

以PID控制器的单闭环直流调速系统传递函数推导可先求出整个系统的开环传递函数，用表示，则开环传递函数如下（理想空载条件下）：

$${G_{pid}}(s) = \frac{{{K_p}{K_s}({K_d}{s^2} + s + {K_i})}}{{{C_e}s({T_s}s + 1){{(s + 1)}^2}({T_a}{T_m}s + {T_m}s + 1)}}$$

将开环传递函数进行闭环运算可以得到闭环传递函数为：

$${\Phi _{pid}}(s) = \frac{{{K_p}{K_s}({K_d}{s^2} + s + {K_i})}}{{\alpha {K_p}{K_s}({K_d}{s^2} + s + {K_i}) + {C_e}s({T_s}s + 1){{(s + 1)}^2}({T_a}{T_m}{s^2} + {T_m}s + 1)}}$$

设、和都为1，并且代入已知参数可以得到系统的闭环传递函数为：

$${\Phi _{pid}}(s) = \frac{{5{s^2} + 5s + 5}}{{7.6754 \times {{10}^{ - 9}}{s^6} + 7.6889 \times {{10}^{ - 5}}{s^5} + 1.4 \times {{10}^{ - 3}}{s^4} + 3.8 \times {{10}^{ - 3}}{s^3} + 0.0188{s^2} + 0.0163s + 0.015}}$$

4、 仿真结果

（1） 基于PI控制器的单闭环直流电机控制系统仿真：

首先创建m脚本文件并输入电机参数、PWM调节器参数和相关的反馈系数，完成后运行脚本，等待右侧工作区出现相关的参数。打开Simulink后新建一个永磁直流电机模型，模型如图4.1所示。

图4.1 永磁直流电机仿真模型

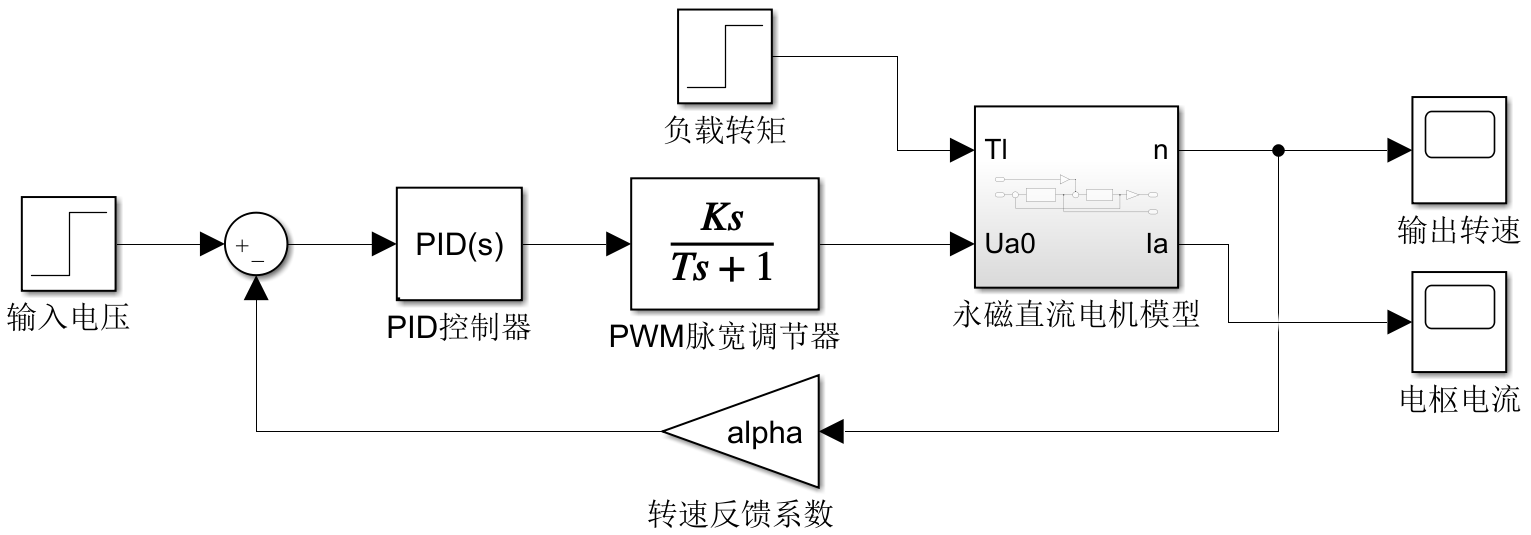
随后搭建外部的控制模型，外部模型如图4.2所示。

图4.2 单闭环直流电机控制仿真模型

输入电压使用单位阶跃响应信号，设置开始时间为0.1s，阶跃电压值为12V；设置负载转矩为单位阶跃响应为0，模拟理想空载下的模型；设置PID控制器的P和I分别为1；考虑到调节器的时间较快，因此设置仿真持续时间为2s；最终得到仿真的转速与电枢电流图如图4.3 4.4所示。

图4.3 仿真转速图（PI）

图4.4 仿真电流图（PI）

对应的根轨迹图与伯德图如图4.5 4.6所示。

图4.5 PI系统的根轨迹图

图4.6 PI系统的伯德图

显然，在一定条件下系统是稳定的。

（2） 基于PID控制器的单闭环直流电机控制系统仿真：

在以上基于PI控制器的单闭环直流电机控制系统的仿真模型中，只需要调节PID控制器中的D参数为1即可改为基于PID控制器的单闭环直流电机控制系统模型，并将检测时间调节为8s，最终得到仿真的转速与电枢电流图如图4.7 4.8所示。

图4.7 仿真转速图（PID）

图4.8 仿真电流图（PID）

对应的根轨迹图与伯德图如图4.9 4.10所示。

图4.9 PID系统的根轨迹图

图4.10 PID系统的伯德图

显然，在一定条件下系统是稳定的。

5、 结果分析

首先从电机的转速上进行讨论，通过以PI作为控制器的单闭环直流电机控制系统转速动态图像（图4.3）可知，其上升时间约为，峰值时间约为，调节时间约为（精度为千分之一秒），超调量约为13.5%。

以PID作为控制器的单闭环直流电机控制系统转速动态图像如图4.6所示，其中不难得到上升时间约为0.117，峰值时间约为，调节时间约为（精度为千分之一秒），超调量约为16.0%。

从上升时间来看，PID控制器整体上升较PI控制器上升较快，不过相对于调节时间与超调量来说，PI控制器的稳定性更好。PID调节器虽然多出一个微分环节但是并没有达到比较理想的效果。从图4.4与4.8来看，PI调节器的电流峰值比PID调节器更低，让它能够保证电机转子不会因为电流过大而烧毁。总体来说PI调节器在单闭环直流电机控制系统中的优势更加明显。

虽然单闭环直流电机控制系统模型采用PI控制器的优势更加明显，但是其峰值电流还是远大于额定电流，因此若加入电流调节环节，就能够更好的保证电机的运行安全。因此采用双闭环直流电机控制系统还是十分有必要的。

参考文献

[1] 胡寿松.自动控制原理(第5版)[M].科学出版社,2007.

[2] 范影乐,杨胜天,李轶.MATLAB仿真应用详解[M].人民邮电出版社,2001.

[3] 张崇巍,李汉强.运动控制系统[M].武汉理工大学出版社,2002.1

[4] 刘陆.基于MATLAB直流电动机控制系统的建模与仿真[J].兰州工业学院学报,2014,21(01):14-17.

[5] 熊颖,乌泽.应用于直流电机控制的PID算法设计[J].电子世界,2020(06):109.

[6] 牛慧敏,常青,王耀力.永磁无刷直流电机调速系统优化控制[J].计算机仿真,2018,35(12):185-190.